8.3 tf in c++
8.3.1 简介
前面内容我们介绍了TF的基本的概念和TF树消息的格式类型,我们知道,TF不仅仅是一个标准、话题,它还是一个接口。本节课我们就介绍c++中TF的一些函数和写法。
8.3.2 数据类型
C++中给我们提供了很多TF的数据类型,如下表:
| 名称 | 数据类型 |
|---|---|
| 向量 | tf::Vector3 |
| 点 | tf::Point |
| 四元数 | tf::Quaternion |
| 3*3矩阵(旋转矩阵) | tf::Matrix3x3 |
| 位姿 | tf::pose |
| 变换 | tf::Transform |
| 带时间戳的以上类型 | tf::Stamped |
| 带时间戳的变换 | tf::StampedTransform |
易混注意:虽然此表的最后带时间戳的变换数据类型为tf::StampedTransform,和上节我们所讲的geometry_msgs/TransformStamped.msg看起来很相似,但是其实数据类型完全不一样,tf::StampedTransform只能用在C++里,只是C++的一个类,一种数据格式,并不是一个消息。而geometry_msgs/TransformStamped.msg是一个message,它依赖于ROS,与语言无关,也即是无论何种语言,C++、Python、Java等等,都可以发送该消息。
8.3.3 数据转换
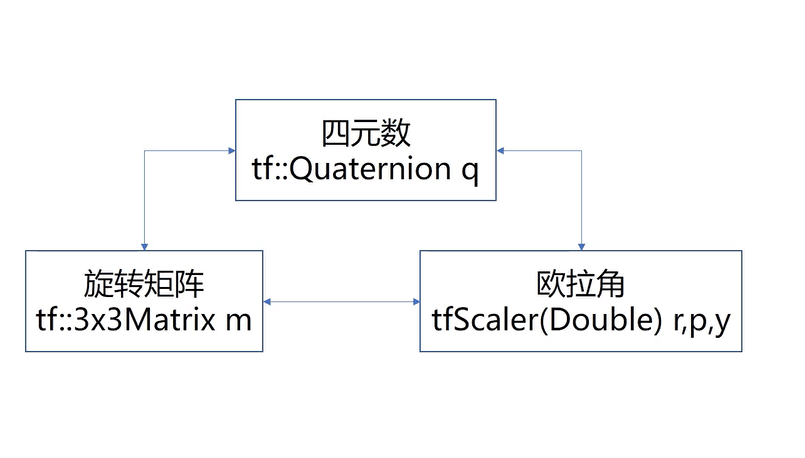
在TF里有可能会遇到各种各样数据的转换,例如常见的四元数、旋转矩阵、欧拉角这三种数据之间的转换。tf in roscpp给了我们解决该问题的函数。详细源码在我们教学课程的代码包中。
首先在tf中与数据转化的数据都类型都包含在#include<tf/tf.h>头文件中,我们将与数据转换相关API都存在tf_demo中的coordinate_transformation.cpp当中,其中列表如下:
第1部分定义空间点和空间向量
| 编号 | 函数名称 | 函数功能 |
|---|---|---|
| 1.1 | tfScalar::tfDot(const Vector3 &v1, const Vector3 &v2) | 计算两个向量的点积 |
| 1.2 | tfScalar length() | 计算向量的模 |
| 1.3 | Vector3 &normalize() | 求与已知向量同方向的单位向量 |
| 1.4 | tfScalar::tfAngle(const Vector3 &v1, const Vector3 &v2) | 计算两个向量的夹角 |
| 1.5 | tfScale::tfDistance(const Vector3 &v1, const Vector3 &v2) | 计算两个向量的距离 |
| 1.6 | tfScale::tfCross(const Vector3 &v1,const Vector3 &v2) | 计算两个向量的乘积 |
示例代码:
#include <ros/ros.h>
#include <tf/tf.h>
//退出用:ctrl+z
int main(int argc, char** argv){
//初始化
ros::init(argc, argv, "coordinate_transformation");
ros::NodeHandle node;
tf::Vector3 v1(1,1,1);
tf::Vector3 v2(1,0,1);
//第1部分,定义空间点和空间向量
std::cout<<"第1部分,定义空间点和空间向量"<<std::endl;
//1.1 计算两个向量的点积
std::cout<<"向量v1:"<<"("<<v1[0]<<","<<v1[1]<<","<<v1[2]<<"),";
std::cout<<"向量v2:"<<"("<<v2[0]<<","<<v2[1]<<","<<v2[2]<<")"<<std::endl;
std::cout<<"两个向量的点积:"<<tfDot(v1,v2)<<std::endl;
//1.2 计算向量的模
std::cout<<"向量v2的模值:"<<v2.length()<<std::endl;
//1.3 求与已知向量同方向的单位向量
tf::Vector3 v3;
v3=v2.normalize();
std::cout<<"与向量v2的同方向的单位向量v3:"<<"("<<v3[0]<<","<<v3[1]<<","<<v3[2]<<")"<<std::endl;
//1.4 计算两个向量的夹角
std::cout<<"两个向量的夹角(弧度):"<<tfAngle(v1,v2)<<std::endl;
//1.5 计算两个向量的距离
std::cout<<"两个向量的距离:"<<tfDistance2(v1,v2)<<std::endl;
//1.6 计算两个向量的乘积
tf::Vector3 v4;
v4=tfCross(v1,v2);
std::cout<<"两个向量的乘积v4:"<<"("<<v4[0]<<","<<v4[1]<<","<<v4[2]<<")"<<std::endl;```
return 0;
}
第2部分定义四元数
| 编号 | 函数名称 | 函数功能 |
|---|---|---|
| 2.1 | setRPY(const tfScalar& yaw, const stScalar &pitch, const tfScalar &roll) | 由欧拉角计算四元数 |
| 2.2 | Vector3 getAxis() | 由四元数得到旋转轴 |
| 2.3 | setRotation(const Vector3 &axis, const tfScalar& angle) | 已知旋转轴和旋转角估计四元数 |
示例代码:
#include <ros/ros.h>
#include <tf/tf.h>
//退出用:ctrl+z
int main(int argc, char** argv){
//初始化
ros::init(argc, argv, "coordinate_transformation");
ros::NodeHandle node;
std::cout<<"第2部分,定义四元数"<<std::endl;
//2.1 由欧拉角计算四元数
tfScalar yaw,pitch,roll;
yaw=0;pitch=0;roll=0;
std::cout<<"欧拉角rpy("<<roll<<","<<pitch<<","<<yaw<<")";
tf::Quaternion q;
q.setRPY(yaw,pitch,roll);
std::cout<<",转化到四元数q:"<<"("<<q[3]<<","<<q[0]<<","<<q[1]<<","<<q[2]<<")"<<std::endl;
//2.2 由四元数得到旋转轴
tf::Vector3 v5;
v5=q.getAxis();
std::cout<<"四元数q的旋转轴v5"<<"("<<v5[0]<<","<<v5[1]<<","<<v5[2]<<")"<<std::endl;
//2.3 由旋转轴和旋转角来估计四元数
tf::Quaternion q2;
q2.setRotation(v5,1.570796);
std::cout<<"旋转轴v5和旋转角度90度,转化到四元数q2:"<<"("<<q2[3]<<","<<q2[0]<<","<<q2[1]<<","<<q2[2]<<")"<<std::endl;
return 0;
}
第3部分定义旋转矩阵
| 编号 | 函数名称 | 函数功能 |
|---|---|---|
| 3.1 | setRotaion(const Quaternion &q) | 通过四元数得到旋转矩阵 |
| 3.2 | getEulerYPR(tfScalar &yaw, tfScalar &pitch, tfScalar &roll ) | 由旋转矩阵求欧拉角 |
示例代码:
#include <ros/ros.h>
#include <tf/tf.h>
//退出用:ctrl+z
int main(int argc, char** argv){
//初始化
ros::init(argc, argv, "coordinate_transformation");
ros::NodeHandle node;
//第3部分,定义旋转矩阵
std::cout<<"第3部分,定义旋转矩阵"<<std::endl;
//3.1 由旋转轴和旋转角来估计四元数
tf::Quaternion q2(1,0,0,0);
tf::Matrix3x3 Matrix;
tf::Vector3 v6,v7,v8;
Matrix.setRotation(q2);
v6=Matrix[0];
v7=Matrix[1];
v8=Matrix[2];
std::cout<<"四元数q2对应的旋转矩阵M:"<<v6[0]<<","<<v6[1]<<","<<v6[2]<<std::endl;
std::cout<<" "<<v7[0]<<","<<v7[1]<<","<<v7[2]<<std::endl;
std::cout<<" "<<v8[0]<<","<<v8[1]<<","<<v8[2]<<std::endl;
//3.2 通过旋转矩阵求欧拉角
tfScalar m_yaw,m_pitch,m_roll;
Matrix.getEulerYPR(m_yaw,m_pitch,m_roll);
std::cout<<"由旋转矩阵M,得到欧拉角rpy("<<m_roll<<","<<m_pitch<<","<<m_yaw<<")"<<std::endl;
return 0;
};
此外,在tf_demo的教学包中,我们还提供常见的欧拉角与四元数的互换,详见Euler2Quaternion.cpp与Quaternion2Euler.cpp Euler2Quaternion.cpp
#include <ros/ros.h>
#include <tf/tf.h>
//退出用:ctrl+z
int main(int argc, char** argv){
//初始化
ros::init(argc, argv, "Euler2Quaternion");
ros::NodeHandle node;
geometry_msgs::Quaternion q;
double roll,pitch,yaw;
while(ros::ok())
{
//输入一个相对原点的位置
std::cout<<"输入的欧拉角:roll,pitch,yaw:";
std::cin>>roll>>pitch>>yaw;
//输入欧拉角,转化成四元数在终端输出
q=tf::createQuaternionMsgFromRollPitchYaw(roll,pitch,yaw);
//ROS_INFO("输出的四元数为:w=%d,x=%d,y=%d,z=%d",q.w,q.x,q.y,q.z);
std::cout<<"输出的四元数为:w="<<q.w<<",x="<<q.x<<",y="<<q.y<<",z="<<q.z<<std::endl;
ros::spinOnce();
}
return 0;
};
Quaternion2Euler.cpp
#include <ros/ros.h>
#include "nav_msgs/Odometry.h"
#include <tf/tf.h>
//退出用:ctrl+z
int main(int argc, char** argv){
//初始化
ros::init(argc, argv, "Quaternion2Euler");
ros::NodeHandle node;
nav_msgs::Odometry position;
tf::Quaternion RQ2;
double roll,pitch,yaw;
while(ros::ok())
{
//输入一个相对原点的位置
std::cout<<"输入的四元数:w,x,y,z:";
std::cin>>position.pose.pose.orientation.w>>position.pose.pose.orientation.x>>position.pose.pose.orientation.y>>position.pose.pose.orientation.z;
//输入四元数,转化成欧拉角数在终端输出
tf::quaternionMsgToTF(position.pose.pose.orientation,RQ2);
// tf::Vector3 m_vector3; 方法2
// m_vector3=RQ2.getAxis();
tf::Matrix3x3(RQ2).getRPY(roll,pitch,yaw);
std::cout<<"输出的欧拉角为:roll="<<roll<<",pitch="<<pitch<<",yaw="<<yaw<<std::endl;
//std::cout<<"输出欧拉角为:roll="<<m_vector3[0]<<",pitch="<<m_vector3[1]<<",yaw="<<m_vector3[2]<<std::endl;
ros::spinOnce();
}
return 0;
};
8.3.4 TF类
tf::TransformBroadcaster类
transformBroadcaster()
void sendTransform(const StampedTransform &transform)
void sendTransform(const std::vector<StampedTransform> &transforms)
void sendTransform(const geometry_msgs::TransformStamped &transform)
void sendTransform(const std::vector<geometry_msgs::TransformStamped> &transforms)
这个类在前面讲TF树的时候提到过,这个broadcaster就是一个publisher,而sendTransform的作用是来封装publish的函数。在实际的使用中,我们需要在某个Node中构建tf::TransformBroadcaster类,然后调用sendTransform(),将transform发布到/tf的一段transform上。/tf里的transform为我们重载了多种不同的函数类型。在我们的tf_demo教学包当中提供了相关的示例代码tf.broadcaster.cpp,具体如下:
#include <ros/ros.h>
#include <tf/transform_broadcaster.h>
#include <tf/tf.h>
//退出用:ctrl+z
int main(int argc, char** argv){
//初始化
ros::init(argc, argv, "tf_broadcaster");
ros::NodeHandle node;
static tf::TransformBroadcaster br;
tf::Transform transform;
//geometry_msgs::Quaternion qw;
tf::Quaternion q;
//定义初始坐标和角度
double roll=0,pitch=0,yaw=0,x=1.0,y=2.0,z=3.0;
ros::Rate rate(1);
while(ros::ok())
{
yaw+=0.1;//每经过一秒开始一次变换
//输入欧拉角,转化成四元数在终端输出
q.setRPY(roll,pitch,yaw);
//qw=tf::createQuaternionMsgFromRollPitchYaw(roll,pitch,yaw);方法2
transform.setOrigin(tf::Vector3(x,y,z));
transform.setRotation(q);
std::cout<<"发布tf变换:sendTransform函数"<<std::endl;
br.sendTransform(tf::StampedTransform(transform,ros::Time::now(),"base_link","link1"));
std::cout<<"输出的四元数为:w="<<q[3]<<",x="<<q[0]<<",y="<<q[1]<<",z="<<q[2]<<std::endl;
// std::cout<<"输出的四元数为:w="<<qw.w<<",x="<<qw.x<<",y="<<qw.y<<",z="<<qw.z<<std::endl;
rate.sleep();
ros::spinOnce();
}
return 0;
};
tf::TransformListener类
void lookupTranform(const std::string &target_frame,const std::string &source_frame,const ros::Time &time,StampedTransform &transform)const
bool canTransform()
bool waitForTransform()const
上一个类是向/tf上发的类,那么这一个就是从/tf上接收的类。首先看lookuptransform()函数,第一个参数是目标坐标系,第二个参数为源坐标系,也即是得到从源坐标系到目标坐标系之间的转换关系,第三个参数为查询时刻,第四个参数为存储转换关系的位置。值得注意,第三个参数通常用ros::Time(0),这个表示为最新的坐标转换关系,而ros::time::now则会因为收发延迟的原因,而不能正确获取当前最新的坐标转换关系。canTransform()是用来判断两个transform之间是否连通,waitForTransform()const是用来等待某两个transform之间的连通,在我们的tf_demo教学包当中提供了相关的示例代码tf_listerner.cpp,具体如下:
#include <ros/ros.h>
#include <tf/transform_listener.h>
#include <geometry_msgs/Twist.h>
int main(int argc, char** argv){
ros::init(argc, argv, "tf_listener");
ros::NodeHandle node;
tf::TransformListener listener;
//1. 阻塞直到frame相通
std::cout<<"1. 阻塞直到frame相通"<<std::endl;
listener.waitForTransform("/base_link","link1",ros::Time(0),ros::Duration(4.0));
ros::Rate rate(1);
while (node.ok()){
tf::StampedTransform transform;
try{
//2. 监听对应的tf,返回平移和旋转
std::cout<<"2. 监听对应的tf,返回平移和旋转"<<std::endl;
listener.lookupTransform("/base_link", "/link1",
ros::Time(0), transform);
//ros::Time(0)表示最近的一帧坐标变换,不能写成ros::Time::now()
}
catch (tf::TransformException &ex) {
ROS_ERROR("%s",ex.what());
ros::Duration(1.0).sleep();
continue;
}
std::cout<<"输出的位置坐标:x="<<transform.getOrigin().x()<<",y="<<transform.getOrigin().y()<<",z="<<transform.getOrigin().z()<<std::endl;
std::cout<<"输出的旋转四元数:w="<<transform.getRotation().getW()<<",x="<<transform.getRotation().getX()<<
",y="<<transform.getRotation().getY()<<",z="<<transform.getRotation().getZ()<<std::endl;
rate.sleep();
}
return 0;
};