附录1 三维空间刚体运动

旋转矩阵

$\quad$在机器人运动的过程当中，我们通常会设定一个惯性坐标系（或者叫世界坐标系），姑且认为这个坐标系是固定不动的。例如：$X_W,Y_W,Z_W$是固定不动的世界坐标系，$X_C,Y_C,Z_C$是机器人坐标系。存在一个向量$P$，在世界坐标系下的坐标是$P_W$，在移动机器人坐标系下的坐标是$P_C$，通常情况下，我们通过传感器已知移动机器人坐标系统下的坐标$P_C$，来求$P$在世界坐标系下的坐标$P_W$

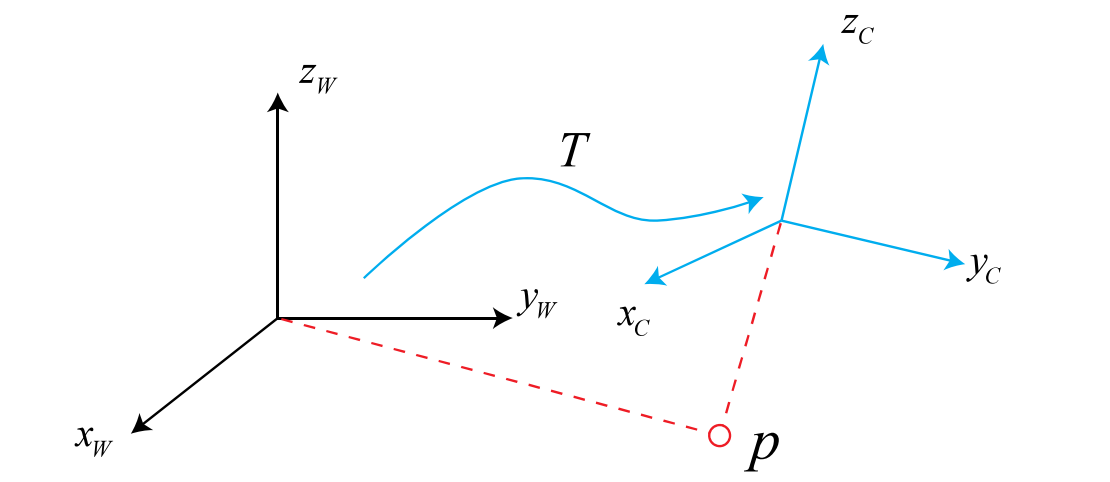
$\quad$为了求$P_W$，我们必须知道机器人坐标系$X_C,Y_C,Z_C$相对与世界坐标$X_W,Y_W,Z_W$做了哪些变换。我们定义世界坐标系经过变换矩阵$T$之后得到机器人坐标系（这可以通过计算里程和IMU的数据进行测量出来）（这也就说明了为什么在机器人刚刚启动的时候odom和base_link坐标系必须是重合的，不然没有办法计算旋转矩阵），另外一般情况下，移动机器人运动是一个刚体运动，也就是说机器人的形状和大小不会因为坐标系不同而改变，这种变换叫做欧式变换。一个欧式变换可以由旋转和平移两个部分组成。首先我们考虑旋转问题，假设在世界坐标系下的单位正交基$(e_x,e_y,e_z)$，在移动机器人坐标系下的单位正交基$(e^"_x,e^"_y,e^"_z)$,那么，根据向量$P$的模可知：

$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad [e_x,e_y,e_z] \cdot P^T_W=[e^"_x,e^"_y,e^"_z] \cdot P^T_C$

$\quad$因此，$P^T_C=[e_x,e_y,e_z]^T \cdot [e^"_x,e^"_y,e^"_z] \cdot P^T_W$，我们将$[e_x,e_y,e_z]^T \cdot [e^"_x,e^"_y,e^"_z]$记做旋转矩阵R，因此上面的表达式可以简化为$P^T_C=R\cdot P^T_W$。接下来是平移部分，假设平移部分是$P^T_{C^"}$经过平移向量t后得到$P^T_{C}$，那么可以得到$P^T_C=P^T_{C^"}+t=R\cdot P^T_w+t$。所以通过旋转矩阵R和平移 向量t，我们可以描述从世界坐标系到移动机器人坐标系的坐标变换。但是这种表达方式存在一个问题，对于连续的位置变换，例如机器人坐标系是随着时间在不断变换的，上面这种表达方式并不是一个线性的表达方式，假设我们经历了两次变换$R_1,t_1$和$R_2,t_2$且满足：从a到b的变换$b=R_1a+t_1$，从b到c的变换$c=R_2b+t_2$.那么从a到c的变换是$c=R_2(R_1a+t_1)+t_2$.并不是我们希望的的形式$c=Ra+t$(然后我们采用齐次坐标的方式进行表达，详细的部分参考李群李代数).